A equação de Bernoulli é um princípio fundamental na área da mecânica dos fluidos que descreve o comportamento de um fluido em movimento dentro de um tubo ou conduto. Ela recebe esse nome em homenagem ao matemático suíço Daniel Bernoulli, que publicou em 1738. A equação de Bernoulli é amplamente utilizada em diversos ramos da engenharia, como na hidrodinâmica, aerodinâmica e na engenharia de sistemas de fluxo de fluidos. Neste artigo, exploraremos os conceitos relacionados à tolerância de Bernoulli, suas aplicações e suas restrições.
Conceitos Iniciais
Antes de discutirmos a equação de Bernoulli em detalhes, é importante compreender alguns conceitos fundamentais da mecânica dos fluidos. Um desses conceitos é o regime permanente , que se refere a um estado em que as propriedades do fluido, como velocidade, densidade e pressão, permanecem constantes em cada ponto ao longo do tempo. Essa condição é essencial para a aplicação da autorização de Bernoulli.
Outro conceito relevante é a transmissão de continuidade , que estabelece que a massa de fluido que flui por uma seção de um tubo é igual à massa que o abandona por outra seção. Isso significa que, em um regime permanente, a massa do fluido não se altera durante o fluxo. Essa observação é fundamental para a compreensão da conservação de massa em sistemas de fluxo de fluidos.
A Equação de Bernoulli para Fluidos Ideais
A equação de Bernoulli para fluidos ideais é formulada considerando um fluido em movimento sob a ação da da gravidade. Ela relaciona a velocidade do fluido, a pressão, a altura em relação a um ponto de referência e a densidade do fluido. Matematicamente, a equação de Bernoulli para fluidos ideais pode ser expressa da seguinte forma:
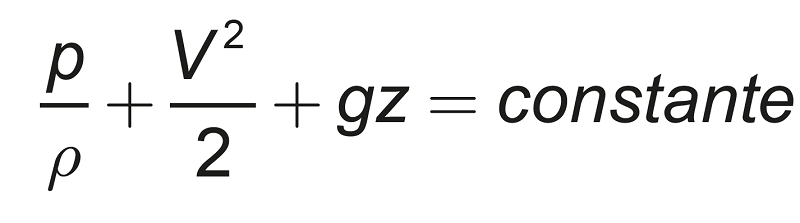
Nessa equação
P representa a pressão do fluido,
ρ é a densidade do fluido,
V é a velocidade do fluido
Z é a altura em relação a um ponto de referência.
A constante na diminuição de Bernoulli indica que a soma dessas grandezas se mantém constante ao longo do fluxo do fluido.
A equação de Bernoulli para fluidos ideais é uma forma de equação de conservação de energia. Ela nos permite estudar o comportamento do fluido em termos de sua energia cinética, energia potencial gravitacional e energia de pressão. Essa tem uma ampla gama de aplicações na engenharia, como no projeto de sistemas de tubulações, na análise de sistemas de distribuição de água e na aerodinâmica de aviões.
A Equação de Bernoulli para Fluidos Reais
Embora a equação de Bernoulli para fluidos seja amplamente utilizada em muitas aplicações, ela não leva em consideração os efeitos da transferência do fluido. Em sistemas com fluidos reais, como água ou ar, é necessário introduzir correções.
Para fluidos reais, a equação de Bernoulli é modificada para incluir o termo da perda de carga devido à admissão. A perda de carga é uma redução de energia devido à fricção entre o fluido e as paredes do tubo. A equação de Bernoulli para fluidos reais pode ser expressa da seguinte forma:
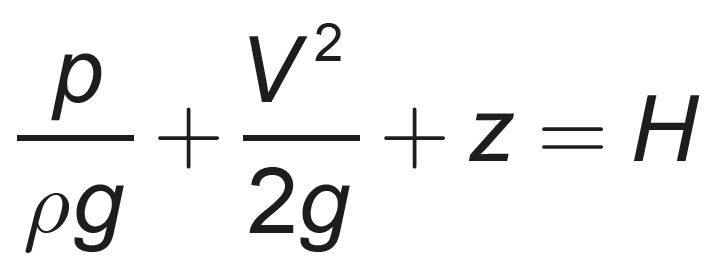
Nessa equação,
H representa a perda carga total do escoamento.
A inclusão desse termo permite uma análise mais precisa do comportamento do fluido em sistemas reais.
Aplicações da Equação de Bernoulli
A equação de Bernoulli tem uma ampla variedade de aplicações práticas. Ela é frequentemente utilizada no projeto e análise de sistemas de fluxo de fluidos, como tubulações, dutos de ar, canais e sistemas de transporte de líquidos. Por exemplo, a equação de Bernoulli é essencial na análise do desempenho de bombas e ventiladores, na medição de vazão em tubulações e na precisão da velocidade do fluxo em bocais e difusores.
Além disso, a equação de Bernoulli é fundamental na compreensão de fenômenos como a sustentação de aviões e a geração de forças em asas de pássaros. Ela explica como a diferença de pressão ao redor de um objeto em movimento pode criar uma força resultante. Essa força é responsável pela sustentação de um avião no ar ou pelo impulso gerado por um asa de pássaro durante o voo.
Limitações da Equação de Bernoulli
Embora a equação de Bernoulli seja uma ferramenta valiosa na análise de sistemas de fluxo de fluidos, é importante destacar suas caracteristicas. A equação de Bernoulli é baseada em algumas suposições simplificadoras, como sistema de fluxo constante, densidade constante, não há realizaçaõ de trabalho sobre ou pelo fluido, não há transferencia de calor para ou a partir do fluido, não há mudaça na energia interna, a equação relaciona dois pontos ao longo de uma linha de fluxo.
Em sistemas com fluidos altamente viscosos, como óleo ou mel, o fluido pode ter um impacto significativo no comportamento do fluxo. Além disso, em situações em que o fluxo é turbulento ou não estacionário, a equação de Bernoulli pode não fornecer resultados precisos. Nessas situações, outras modelos matemático mais complexos devem ser utilizados para uma análise mais precisa.
Conclusão
A equação de Bernoulli é uma ferramenta poderosa na mecânica dos fluidos, que permite analisar o comportamento dos fluidos em movimento dentro de um tubo ou conduto. Ela é fundamental para o projeto e análise de sistemas de fluxo de fluidos, como tubulações e sistemas de distribuição de água. No entanto, é importante ter em mente suas restrições e considerar outras alternativas e modelos mais avançados em situações que fogem das suposições simplificadoras da equação de Bernoulli.
Neste artigo, exploramos os conceitos fundamentais relacionados à equação de Bernoulli, suas aplicações e suas restrições. Espero que você tenha adquirido um melhor entendimento sobre esse importante princípio da mecânica dos fluidos.
Para saber mais veja os posts:
O Número de Reynolds: Uma Medida Fundamental na Mecânica dos Fluidos